Global: The time value of money (TVM)

Στόχοι Μαθήματος:

  1. Understand the principle of the Time Value of Money (TVM), which posits that money available now is worth more than the same amount in the future due to its potential earning capacity.

  2. Learn the formulas and applications for calculating Present Value (PV) και Future Value (FV), essential tools for evaluating the worth of future cash flows in today’s dollars and projecting the growth of current investments over time.

  3. Explore how επιτόκια και πληθωρισμός influence PV and FV calculations, particularly within different economic environments, affecting investment returns and financial planning.

  4. Recognize the practical implications of PV and FV in real-world scenarios, such as retirement planning, saving strategies, and assessing the financial viability of investment opportunities.

A. Introduction

ο time value of money (TVM) is a fundamental financial concept that asserts money available today is worth more than the same amount in the future due to its earning potential. This principle forms the foundation for various financial decisions, from investment planning to loan structuring. Understanding the present value και future value of money allows investors and financial professionals to evaluate opportunities and make informed decisions about where to allocate resources.

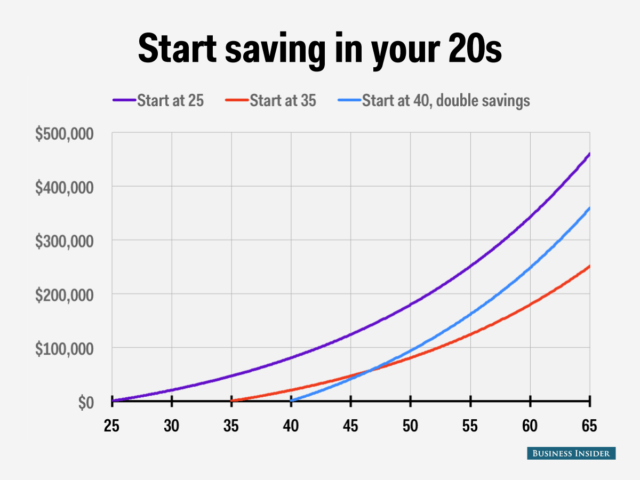
 Εικόνα: Start Saving in Your 20s

 Περιγραφή:

 

This line chart demonstrates the potential growth of savings when starting at different ages: 25, 35, και 40 (with double the savings rate). The vertical axis represents the total savings accumulated (up to $500,000), while the horizontal axis shows age progression from 25 to 65. The chart highlights the impact of ανατοκισμός over time, with the purple line representing savings started at 25, the red line at 35, και το blue line at 40 (doubling the savings rate). The early starter accumulates the most wealth, showcasing the importance of starting early for maximizing growth.

 

 Βασικά συμπεράσματα:

 

  • Early savings (starting at 25) lead to the highest accumulated amount due to longer compounding periods.
  • Starting at 35 shows less growth than starting at 25, emphasizing the value of starting sooner.
  • Doubling savings at 40 still results in lower total savings compared to starting at 25, demonstrating that time is more critical than the savings rate in maximizing returns.

 

 Εφαρμογή πληροφοριών: 

 

Κατανοώντας το power of compounding και το time value of money can encourage individuals to start saving as early as possible. By doing so, they can maximize returns with a smaller initial investment compared to starting later. This data serves as a reminder to prioritize savings early in life, reinforcing the importance of long-term financial planning for investors and learners.

 

B. Present Value

Present value (PV) represents the current worth of a sum of money to be received or paid in the future, discounted back to today’s terms. This concept helps investors assess how much future cash flows are worth in today’s terms, based on a given interest rate or discount rate.

 

Formula: Present Value = Future Value / (1 + r)^n

Where:

    • Future Value (FV): The value of money in the future.
    • r: The interest or discount rate.
    • n: The number of periods.

 

For example, if an investor expects to receive €1,000 in 5 years and the discount rate is 5%, the present value would be:

 

  • PV = €1,000 / (1 + 0.05)^5 = €783.53.

 

This means that €1,000 in 5 years is equivalent to about €783.53 today, given a 5% interest rate. Investors use the present value concept to determine the value of future cash flows, whether they are from investments, loans, or other financial commitments.

 

C. Future Value

Future value (FV) refers to the amount of money an investment will grow to over a specific period, given a certain interest rate or rate of return. It helps investors understand how much an initial sum will be worth at a future date if it is invested or earns interest over time.

  • Formula: Future Value = Present Value × (1 + r)^n

    Where:
    • Present Value (PV): The initial sum of money.
    • r: The interest or growth rate.
    • n: The number of periods.

 

For example, if an investor places €500 into an account that earns 4% interest annually, the future value after 10 years would be:

  • FV = €500 × (1 + 0.04)^10 = €740.12.

 

This calculation shows how money can grow over time, making it useful for financial planning, including retirement savings and investment decisions.

D. Key Takeaways

  1. Διαχρονική αξία του χρήματος: Money today is worth more than the same amount in the future due to its potential to earn returns. This principle drives investment decisions and financial planning.

  2. Παρούσα αξία: Present value discounts future cash flows to today’s terms, allowing for the evaluation of future investments and obligations based on current value.

  3. Future Value: Future value calculates how much an investment made today will be worth in the future, based on a given interest rate or rate of return.

  4. Practical Application: Understanding both present and future value helps individuals and businesses make informed decisions about savings, investments, and financial obligations.

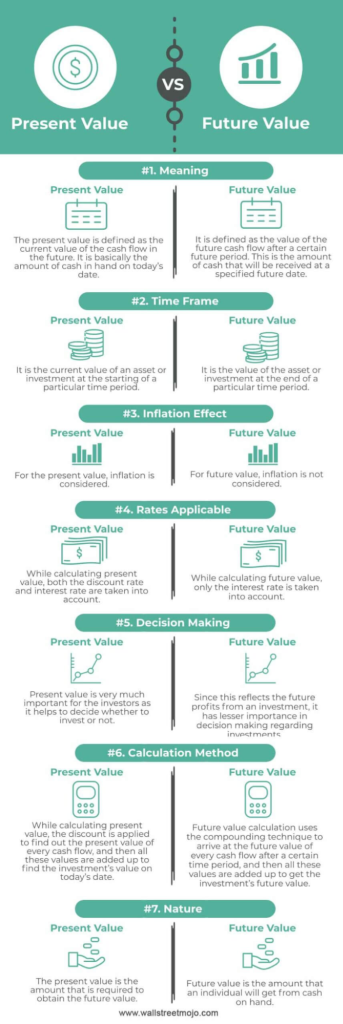
 Εικόνα: Present Value vs Future Value

 Περιγραφή:

 

This infographic compares Παρούσα αξία (PV) and Future Value (FV) based on seven aspects: Meaning, Time Frame, Inflation Effect, Rates Applicable, Decision Making, Calculation Method, και Nature. PV is the current worth of a future cash flow, accounting for inflation and the discount rate, while FV represents the amount of money that will be available at a specified time in the future, factoring in interest rates and compounding. The comparison highlights key differences, such as how PV includes inflation effects while FV does not, and how each is used for different decision-making processes.

 

 Βασικά συμπεράσματα:

 

 

  • Present Value (PV) reflects the current value of future cash flows, while Future Value (FV) indicates what the cash flows will be worth in the future.
  • PV includes inflation and discount rates, making it vital for επενδυτικές αποφάσεις.
  • FV emphasizes the compounding effect and is used to estimate future profits.
  • PV calculation uses the discount rate, while FV calculation relies on the interest rate.

 

 Εφαρμογή πληροφοριών: 

 

Investors and learners can use the concepts of PV and FV to evaluate different investment opportunities. PV is particularly useful for determining whether an investment is worthwhile based on its current worth, while FV helps estimate potential future returns. Understanding these concepts aids in οικονομικός προγραμματισμός, προϋπολογισμός, και investment analysis by providing clarity on the time value of money and the effects of interest rates.

 

συμπέρασμα

ο time value of money is a critical concept in finance that impacts investment decisions, savings strategies, and loan assessments. By understanding present value και future value, investors can evaluate opportunities, compare financial options, and make informed decisions about where to allocate resources for the best returns.

Βασικές πληροφορίες μαθήματος:

  1. Present Value (PV) helps determine the current worth of a future sum of money or stream of cash flows given a specific rate of return. This calculation is crucial for comparing the value of investments that offer returns at different times.

  2. Future Value (FV) illustrates the value of an initial investment after applying the rate of growth over a period. This is crucial for investors aiming to understand how their current savings or investments will accumulate over time.

  3. ο impact of compounding on savings is significant, as demonstrated by scenarios that compare starting ages for investment. This emphasizes the advantage of early investment due to the exponential growth potential of compound interest.

  4. Practical application of these concepts in personal financial planning involves using PV and FV to make educated decisions about loans, savings, retirement funds, and other long-term financial commitments.

Τελική δήλωση:

Mastery of Present Value and Future Value calculations is fundamental for anyone engaged in financial decision-making. These concepts not only enhance understanding of investment potential and financial planning but also underscore the importance of starting financial endeavors early to capitalize on the benefits of compound interest.

Προηγούμενο Lesson
Επιστροφή στο Course
Επόμενο Lesson

Αφήστε ένα σχόλιο